Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Penyelesaian SPtLDV
Pada
topik sebelumnya, kalian telah mempelajari topik sistem persamaan
linear dua variabel dan tiga variabel. Sekarang, kita akan mempelajari
topik sistem pertidaksamaan linear dua variabel.
1. PERTIDAKSAMAAN LINEAR DUA VARIABEL
Pertidaksamaan linear dua variabel adalah suatu pertidaksamaan yang memuat dua variabel dan setiap variabel berderajat paling tinggi satu. Sedangkan tanda pertidaksamaan adalah >, <, ≤, dan ≥.
Contoh pertidaksamaan linear dua variabel :

2. SISTEM PERTIDAKSAMAAN LINEAR DUA VARIABEL
Sistem pertidaksamaan linear dua variabel adalah suatu sistem yang terdiri dari dua atau lebih pertidaksamaan linear dua variabel dengan variabel-variabel yang sama.
Contoh sistem pertidaksamaan linear dua variabel :
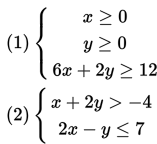
Contoh berikut ini **bukan** merupakan sistem pertidaksamaan linear dua variabel, karena variabel yang digunakan tidak sama.

Penyelesaian sistem pertidaksamaan linear dua variabel adalah irisan daerah penyelesaian pertidaksamaan linear dua variabel yang membentuknya.
Langkah-langkah menentukan daerah penyelesaian sistem pertidaksamaan linear dua variabel :
Contoh 1
Gambarlah daerah penyelesaian sistem pertidaksamaan x + 2y > -4, 2x – y ≤ 3 dengan mengarsir daerah penyelesaian!
Penyelesaian
Langkah-langkah penyelesaian :
(i) Menggambar garis pembatas
x +2 y > -4 adalah garis x + 2y = – 4 yang melalui titik (– 4, 0) dan (0,– 2)
2x – y ≤ 3 adalah garis 2x – y = 3 yang melalui titik (1 ½ , 0) dan (0,– 3)
(ii) Penentuan daerah penyelesaiannya dengan cara mengarsir daerah penyelesaian tersebut
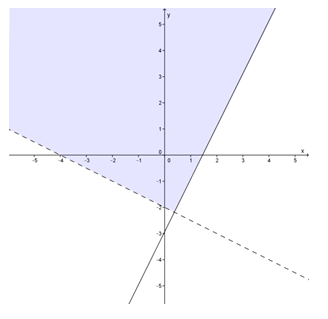
Contoh 2
Gambarlah daerah penyelesaian sistem pertidaksamaan x ≥ 0 ; x + y ≥ 3 ; 2x + y ≤ 4 dengan mengarsir daerah penyelesaian!
Penyelesaian
Langkah-langkah penyelesaian :
(i) Menggambar garis pembatas
x ≥ 0 adalah garis x =0 yaitu sumbu y
x + y ≥ 3 adalah garis x + y = 3 yang melalui titik (3, 0) dan (0, 3)
2x + y ≤ 4 adalah garis 2x + y = 4 yang melalui titik (2, 0) dan (0, 4)
(ii) Penentuan daerah penyelesaiannya dengan cara mengarsir daerah penyelesaian tersebut
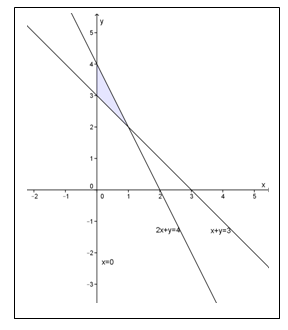
Menentukan sistem pertidaksamaan linear dua variabel dari suatu daerah penyelesaian yang diketahui
Langkah 1 : menentukan persamaan garis pembatasnya
a. Persamaan garis melalui titik (x1, y1) dan (x2, y2)
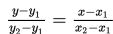
b. Persamaan garis melalui titik (x1, y1) dengan gradien m -> y – y1 = m (x – x1)
c. Persamaan garis melalui titik (a, 0) dan (0, b)
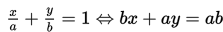
Langkah 2 : Ambil sebuah titik uji yang diujikan pada persamaan garis tersebut kemudian beri tanda pertidaksamaan sesuai hasil uji tersebut
Contoh 3
Perhatikan gambar berikut ini dan tentukan sistem pertidaksamaan dari daerah yang diarsir!
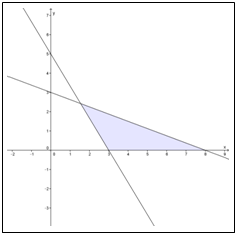
Penyelesaian
Langkah 1
Daerah penyelesaian dibatasi 3 garis yaitu
1. Garis sumbu x, persamaannya y = 0
2. Garis yang melalui titik (0,5) dan (3,0), persamaannya 5x +3y = 15
3. Garis yang melalui titik (0,3) dan (8,0), persamaannya 3x + 8y = 24
Langkah 2
Menentukan pertidaksamaan yang memenuhi daerah penyelesaian (daerah yang diarsir)
• y = 0 → y ≥ 0
• 3x + 8y = 24 → 3x + 8y ≤ 24
• 5x + 3y = 15 → 5x + 3y ≥ 15
Jadi, sistem pertidaksamaan yang berlaku adalah : y ≥ 0; 3x + 8y ≤ 24, 5x + 3y ≥ 15
1. PERTIDAKSAMAAN LINEAR DUA VARIABEL
Pertidaksamaan linear dua variabel adalah suatu pertidaksamaan yang memuat dua variabel dan setiap variabel berderajat paling tinggi satu. Sedangkan tanda pertidaksamaan adalah >, <, ≤, dan ≥.
Contoh pertidaksamaan linear dua variabel :

2. SISTEM PERTIDAKSAMAAN LINEAR DUA VARIABEL
Sistem pertidaksamaan linear dua variabel adalah suatu sistem yang terdiri dari dua atau lebih pertidaksamaan linear dua variabel dengan variabel-variabel yang sama.
Contoh sistem pertidaksamaan linear dua variabel :
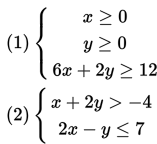
Contoh berikut ini **bukan** merupakan sistem pertidaksamaan linear dua variabel, karena variabel yang digunakan tidak sama.

Penyelesaian sistem pertidaksamaan linear dua variabel adalah irisan daerah penyelesaian pertidaksamaan linear dua variabel yang membentuknya.
Langkah-langkah menentukan daerah penyelesaian sistem pertidaksamaan linear dua variabel :
- Gambarlah grafik garis dari setiap pertidaksamaan linear dua variabel yang diberikan dalam sistem pertidaksamaan linear dua variabel pada satu diagram Cartesius
- Ambil satu titik uji untuk mengetahui daerah penyelesaian setiap pertidaksamaan linear dua variabelnya, kemudian arsirlah daerah penyelesaian.
- Daerah penyelesaian sistem pertidaksamaan linear yaitu irisan dari daerah penyelesaian pertidaksamaan linear dua variabel yang membentuknya.
Contoh 1
Gambarlah daerah penyelesaian sistem pertidaksamaan x + 2y > -4, 2x – y ≤ 3 dengan mengarsir daerah penyelesaian!
Penyelesaian
Langkah-langkah penyelesaian :
(i) Menggambar garis pembatas
x +2 y > -4 adalah garis x + 2y = – 4 yang melalui titik (– 4, 0) dan (0,– 2)
2x – y ≤ 3 adalah garis 2x – y = 3 yang melalui titik (1 ½ , 0) dan (0,– 3)
(ii) Penentuan daerah penyelesaiannya dengan cara mengarsir daerah penyelesaian tersebut

Contoh 2
Gambarlah daerah penyelesaian sistem pertidaksamaan x ≥ 0 ; x + y ≥ 3 ; 2x + y ≤ 4 dengan mengarsir daerah penyelesaian!
Penyelesaian
Langkah-langkah penyelesaian :
(i) Menggambar garis pembatas
x ≥ 0 adalah garis x =0 yaitu sumbu y
x + y ≥ 3 adalah garis x + y = 3 yang melalui titik (3, 0) dan (0, 3)
2x + y ≤ 4 adalah garis 2x + y = 4 yang melalui titik (2, 0) dan (0, 4)
(ii) Penentuan daerah penyelesaiannya dengan cara mengarsir daerah penyelesaian tersebut

Menentukan sistem pertidaksamaan linear dua variabel dari suatu daerah penyelesaian yang diketahui
Langkah 1 : menentukan persamaan garis pembatasnya
a. Persamaan garis melalui titik (x1, y1) dan (x2, y2)
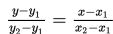
b. Persamaan garis melalui titik (x1, y1) dengan gradien m -> y – y1 = m (x – x1)
c. Persamaan garis melalui titik (a, 0) dan (0, b)
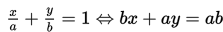
Langkah 2 : Ambil sebuah titik uji yang diujikan pada persamaan garis tersebut kemudian beri tanda pertidaksamaan sesuai hasil uji tersebut
Contoh 3
Perhatikan gambar berikut ini dan tentukan sistem pertidaksamaan dari daerah yang diarsir!

Penyelesaian
Langkah 1
Daerah penyelesaian dibatasi 3 garis yaitu
1. Garis sumbu x, persamaannya y = 0
2. Garis yang melalui titik (0,5) dan (3,0), persamaannya 5x +3y = 15
3. Garis yang melalui titik (0,3) dan (8,0), persamaannya 3x + 8y = 24
Langkah 2
Menentukan pertidaksamaan yang memenuhi daerah penyelesaian (daerah yang diarsir)
• y = 0 → y ≥ 0
• 3x + 8y = 24 → 3x + 8y ≤ 24
• 5x + 3y = 15 → 5x + 3y ≥ 15
Jadi, sistem pertidaksamaan yang berlaku adalah : y ≥ 0; 3x + 8y ≤ 24, 5x + 3y ≥ 15

SHARE

0 Komentar
Post a Comment
Berikan pendapat Anda tentang materi yang kami sajikan!