Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Model Matematika yang memuat SPLTV
Dalam
kehidupan sehari-hari, kita sering dihadapkan pada permasalahan yang
dapat diterjemahkan dalam model matematika yang berbentuk sistem
persamaan. Pada materi ini, kita akan mempelajari cara membuat model
matematika yang berhubungan dengan sistem persamaan linear tiga
variabel.
Langkah-langkah yang harus dilakukan untuk membuat model matematika adalah sebagai berikut:
Masa kehamilan rata-rata (dalam hari) dari gajah, sapi, dan kuda apabila dijumlahkan adalah 1.260 hari. Masa kehamilan kuda adalah 60 hari lebih lama daripada sapi. Dua kali masa kehamilan kuda kemudian dikurangi 40 merupakan masa kehamilan gajah. Berapa hari masa kehamilan dari masing-masing hewan tersebut?
Pembahasan
Kita misalkan x adalah masa kehamilan gajah, y adalah masa kehamilan sapi, dan z adalah masa kehamilan kuda.
Jumlah rata-rata masa kehamilan gajah, sapi, dan kuda jika dijumlahkan 1.260 hari, sehingga persamaan yang diperoleh adalah :
x + y + z = 1260 ... (1)
Masa kehamilan kuda adalah 60 hari lebih lama daripada sapi
-> z = y + 60 ... (2)
Dua kali masa kehamilan kuda kemudian dikurangi 40 merupakan masa kehamilan gajah
-> x = 2z – 40 ... (3)
Ketiga persamaan tersebut membentuk sistem persamaan linear sebagai berikut :
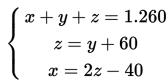
Jika persamaan tersebut kita ubah ke dalam bentuk standar, sistem tersebut menjadi :
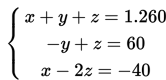
Eliminasi suku z pada persamaan (1) dan (2)
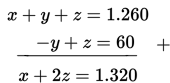
Hasil eliminasi ini kemudian dieliminasi lagi dengan persamaan (3)
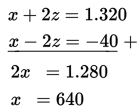
Substitusikan nilai x ke persamaan (3)
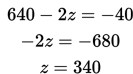
Substitusikan nilai z ke persamaan (2)
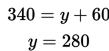
Dengan demikian, penyelesaian dari sistem persamaan ini adalah
x = 640, y = 280, dan z = 340
Jadi dapat kita simpulkan bahwa masa kehamilan rata-rata dari gajah adalah 640 hari, sapi 280 hari, dan kuda 340 hari.
Langkah-langkah yang harus dilakukan untuk membuat model matematika adalah sebagai berikut:
- nyatakan besaran yang ada sebagai variabel dalam sistem persamaan
- modelkan variabel-variabel tersebut dalam suatu persamaan dengan mengingat syarat-syarat berlakunya variabel
- selesaikan model matematika yang telah dibuat
- tafsirkan hasil yang diperoleh dari permasalahan yang ada
Masa kehamilan rata-rata (dalam hari) dari gajah, sapi, dan kuda apabila dijumlahkan adalah 1.260 hari. Masa kehamilan kuda adalah 60 hari lebih lama daripada sapi. Dua kali masa kehamilan kuda kemudian dikurangi 40 merupakan masa kehamilan gajah. Berapa hari masa kehamilan dari masing-masing hewan tersebut?
Pembahasan
Kita misalkan x adalah masa kehamilan gajah, y adalah masa kehamilan sapi, dan z adalah masa kehamilan kuda.
Jumlah rata-rata masa kehamilan gajah, sapi, dan kuda jika dijumlahkan 1.260 hari, sehingga persamaan yang diperoleh adalah :
x + y + z = 1260 ... (1)
Masa kehamilan kuda adalah 60 hari lebih lama daripada sapi
-> z = y + 60 ... (2)
Dua kali masa kehamilan kuda kemudian dikurangi 40 merupakan masa kehamilan gajah
-> x = 2z – 40 ... (3)
Ketiga persamaan tersebut membentuk sistem persamaan linear sebagai berikut :
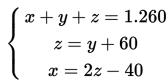
Jika persamaan tersebut kita ubah ke dalam bentuk standar, sistem tersebut menjadi :
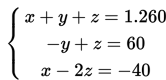
Eliminasi suku z pada persamaan (1) dan (2)
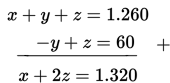
Hasil eliminasi ini kemudian dieliminasi lagi dengan persamaan (3)
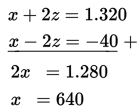
Substitusikan nilai x ke persamaan (3)
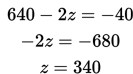
Substitusikan nilai z ke persamaan (2)
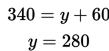
Dengan demikian, penyelesaian dari sistem persamaan ini adalah
x = 640, y = 280, dan z = 340
Jadi dapat kita simpulkan bahwa masa kehamilan rata-rata dari gajah adalah 640 hari, sapi 280 hari, dan kuda 340 hari.

SHARE

0 Komentar
Post a Comment
Berikan pendapat Anda tentang materi yang kami sajikan!