Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Menyelesaikan Sistem Persamaan Linear Dengan Menggunakan Grafik
The
solution of a system of linear equations is the point that satisfies
all the equations in the system. Graphically, a linear equation
represents a straight line where the points on the line are the points
that satisfy the linear equation. So, for a system of linear equations
the solution will be the point that lies on all the lines i.e. satisfies
all the equations. Therefore, it can be said that the solution of a
system of linear equations is the point of intersection of all the lines
in that system. For example consider a system of linear equations:
 As two distinct straight lines cannot intersect each other more than
once, it implies that a system of two or more distinct linear equations
can have a maximum of one solution where all the equations are
satisfied. Similarly, if two equations have the same slope then they
represent two parallel lines. As, two parallel lines do not touch or
intersect each other, such a system of linear equations has no
solution.
As two distinct straight lines cannot intersect each other more than
once, it implies that a system of two or more distinct linear equations
can have a maximum of one solution where all the equations are
satisfied. Similarly, if two equations have the same slope then they
represent two parallel lines. As, two parallel lines do not touch or
intersect each other, such a system of linear equations has no
solution.
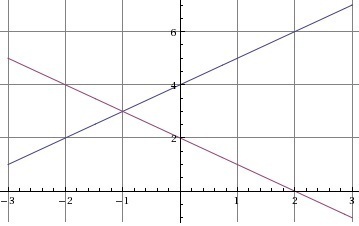
 It can be observed from the above graph that the two lines intersect each other at the point where x=1 and y=6.
It can be observed from the above graph that the two lines intersect each other at the point where x=1 and y=6.
 It is apparent from the figure that the lines are parallel and will
never intersect each other hence the graphical method tells us that the
solution does not exist. It can be verified analytically as:
It is apparent from the figure that the lines are parallel and will
never intersect each other hence the graphical method tells us that the
solution does not exist. It can be verified analytically as:
y = x + 4
y = -x + 2
By
substitution, the solution is calculated as (x=3 and y=-1) which is
also the point of intersection of the two lines, as shown in the
following figure:

The solution of a system of linear equations can be
determined by plotting the lines and finding their point of
intersections. Following examples illustrate the method of solving the
systems of linear equations graphically:
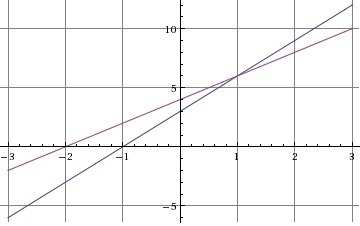
Example 1:
Solve the system of linear equations:
y = 3x + 3
y = 2x + 4
To find the solution both the equations must be plotted on the same graph. The plot of both these equations will be as follows:

This can be verified by analytical methods as:
Verification:
y = 3x + 3
y = 2x + 4
So,
3x + 3 = 2x + 4
3x - 2x = 4 - 3
x = 1
Substituting in y = 3x + 3
y = 3(1) + 3 = 3 + 3
y = 6
So the solution is x=1 and y=6.
If the two lines do not intersect each other then they do not have a
valid solution. For example, consider the following system of linear
equations:
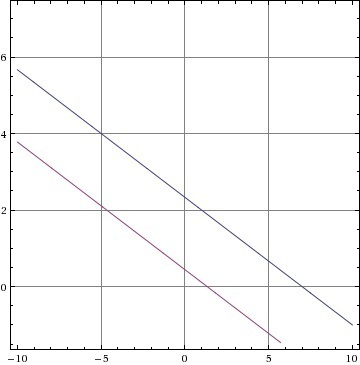
Example 2:
x + 3y = 7
3x + 9y = 4
These two equations are plotted in the following graph:

Verification:
x + 3y = 7 => x = 7-3y
substituting in the other equation
3(7 - 3y) + 9y = 4
21 - 9y + 9y = 4
21 = 4 (not true)
Hence, the solution does not exist

SHARE

0 Komentar
Post a Comment
Berikan pendapat Anda tentang materi yang kami sajikan!