Persamaan dan Pertidaksamaan Nilai Mutlak: Persamaan Nilai Mutlak
June 01, 2016
1
Pada topik sebelumnya, kalian telah belajar mengenai konsep nilai
mutlak. Sedangkan pada topik ini kalian akan mempelajari persamaan dalam
bentuk nilai mutlak.
Berdasarkan definisi nilai mutlak pada topik sebelumnya, tentunya kalian masih ingat bahwa untuk setiap x bilangan real berlaku :
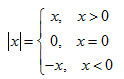 Seperti yang telah kalian ketahui, persamaan adalah kalimat matematika terbuka yang menyatakan hubungan sama dengan dan ditulis = . Dengan demikian, persamaan nilai mutlak adalah persamaan dalam bentuk nilai mutlak.
Seperti yang telah kalian ketahui, persamaan adalah kalimat matematika terbuka yang menyatakan hubungan sama dengan dan ditulis = . Dengan demikian, persamaan nilai mutlak adalah persamaan dalam bentuk nilai mutlak.
Mari kita cermati beberapa bentuk persamaan nilai mutlak berikut :
 Untuk memperdalam pemahaman kalian, mari kita cermati beberapa contoh berikut :
Untuk memperdalam pemahaman kalian, mari kita cermati beberapa contoh berikut :
Contoh 1 Tentukan Himpunan penyelesaian dari |x| = 6
Penyelesaian
|x| = 6 ⟺ x = 6 atau x = – 6
Himpunan penyelesaiannya adalah {– 6 , 6}.
Contoh 2 Tentukan himpunan penyelesaian dari persamaan |2p| = 18
Penyelesaian:
|2p| = 18 ⟺ 2p = 18 atau 2p = – 18 ⟺ p = 9 atau p = – 9
Himpunan penyelesaiannya adalah {– 9 , 9}.
Contoh 3 Tentukan himpunan penyelesaian dari persamaan | x – 4| = 7
Penyelesaian
|x – 4| = 7 ⟺ x – 4 = 7 atau x – 4 = – 7 ⟺ x = 11 atau x = – 3
Himpunan penyelesaiannya adalah {– 3 , 11}.
Contoh 4 Tentukan himpunan penyelesaian dari persamaan |5x + 3| = |2x|
Penyelesaian
|5x + 3| = |2x|
⟺ 5x + 3 = 2x atau 5x + 3 = –(2x)
⟺ 3x = – 3 atau 5x + 3 = – 2x
⟺ x = – 1 atau 7x = – 3
⟺ x = 1 atau x = -3/7
Himpunan penyelesaiannya adalah {-1 , -3/7}
Berdasarkan definisi nilai mutlak pada topik sebelumnya, tentunya kalian masih ingat bahwa untuk setiap x bilangan real berlaku :
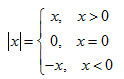
Mari kita cermati beberapa bentuk persamaan nilai mutlak berikut :

Contoh 1 Tentukan Himpunan penyelesaian dari |x| = 6
Penyelesaian
|x| = 6 ⟺ x = 6 atau x = – 6
Himpunan penyelesaiannya adalah {– 6 , 6}.
Contoh 2 Tentukan himpunan penyelesaian dari persamaan |2p| = 18
Penyelesaian:
|2p| = 18 ⟺ 2p = 18 atau 2p = – 18 ⟺ p = 9 atau p = – 9
Himpunan penyelesaiannya adalah {– 9 , 9}.
Contoh 3 Tentukan himpunan penyelesaian dari persamaan | x – 4| = 7
Penyelesaian
|x – 4| = 7 ⟺ x – 4 = 7 atau x – 4 = – 7 ⟺ x = 11 atau x = – 3
Himpunan penyelesaiannya adalah {– 3 , 11}.
Contoh 4 Tentukan himpunan penyelesaian dari persamaan |5x + 3| = |2x|
Penyelesaian
|5x + 3| = |2x|
⟺ 5x + 3 = 2x atau 5x + 3 = –(2x)
⟺ 3x = – 3 atau 5x + 3 = – 2x
⟺ x = – 1 atau 7x = – 3
⟺ x = 1 atau x = -3/7
Himpunan penyelesaiannya adalah {-1 , -3/7}

SHARE

|x+1| = |3-x|
ReplyDeleteBagaimana cara mengerjakan soal sepwrti itu?